Poster #092, Earthquake Forecasting and Predictability (EFP)

Covariance Analysis of the UCERF3-TI Logic Tree

Jared T. Santa Maria, Luis Vazquez, & Thomas H. Jordan
Poster Image: 

Poster Presentation

2020 SCEC Annual Meeting, Poster #092, SCEC Contribution #10566 VIEW PDF
The epistemic uncertainties in the event-rate vector lambda of the time-independent Uniform California Earthquake Rupture Forecast (UCERF3-TI) are represented by a weighted logic tree with K = 7 branching levels and L = 1440 leaves (Field et al. 2014). At each branching level k = 1, … , K, the array of model-component choices, as well as their assigned weights, are the same for every vertex, so that the subtrees of the vertices at any given level are replications of a weighted subtree template. In this study, we use this replicated structure to investigate correlations among the rate values imposed by the model-component choices included in the logic tree. 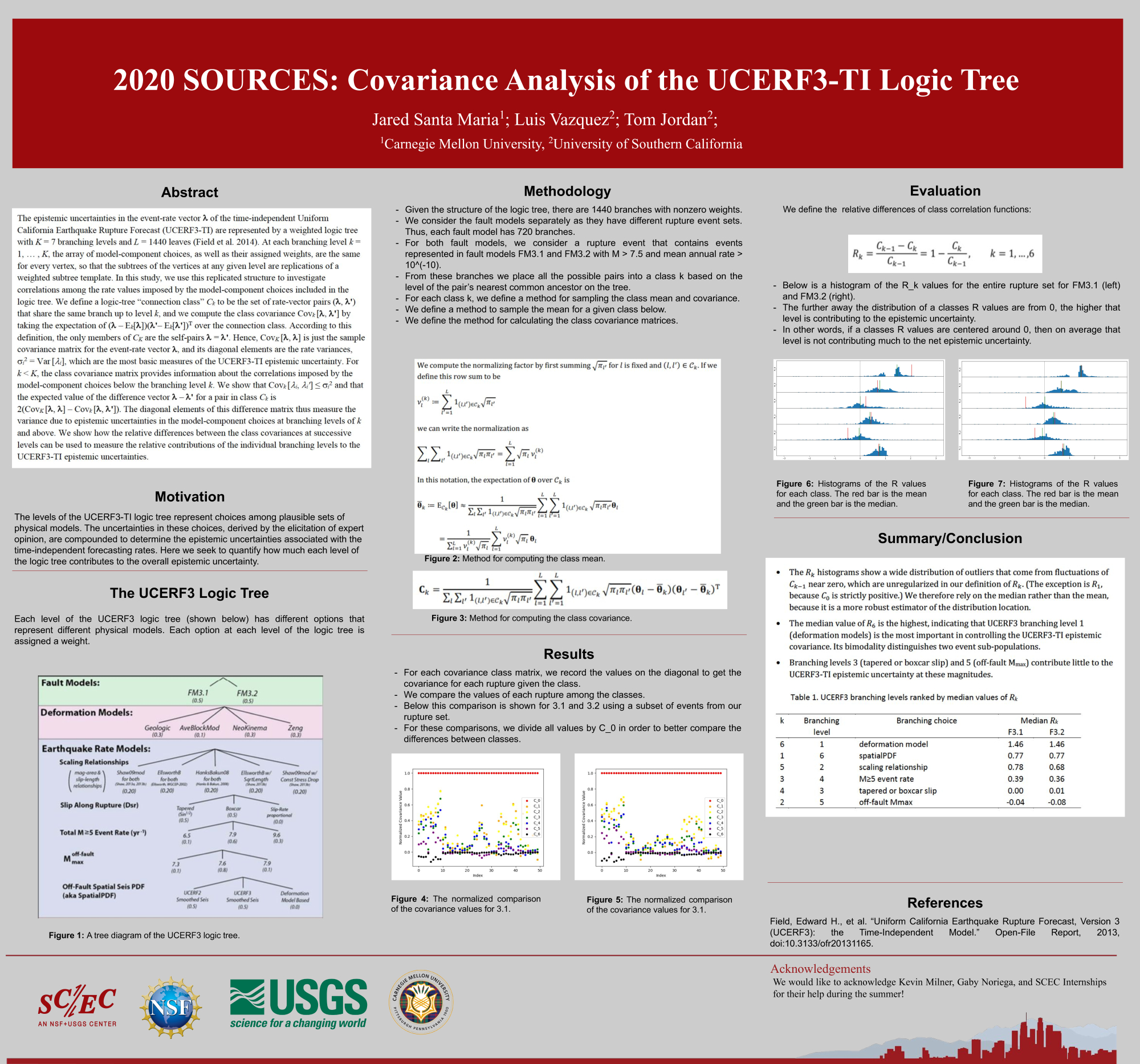We define a logic-tree “connection ...class” C_k to be the set of rate-vector pairs (lambda, lambda') that share the same branch up to level k, and we compute the class covariance Cov_k [lambda, lambda'] by taking the expectation of (lambda – E_k[lambda]) (lambda'– E_k [lambda'])^T over the connection class. According to this definition, the only members of C_K are the self-pairs lambda = lambda'. Hence, Cov_K [lambda, lambda] is just the sample covariance matrix for the event-rate vector lambda, and its diagonal elements are the rate variances, (sigma_i)^2 = Var [lambda_i], which are the most basic measures of the UCERF3-TI epistemic uncertainty. For k < K, the class covariance matrix provides information about the correlations imposed by the model-component choices below the branching level k. We show that Cov_k [lambda_i, lambda_i'] ≤ (sigma_i)^2 and that the expected value of the difference vector lambda – lambda' for a pair in class C_k is 2(Cov_K [lambda, lambda] – Covk [lambda, lambda']). The diagonal elements of this difference matrix thus measure the variance due to epistemic uncertainties in the model-component choices at branching levels of k and above. We use this graph-theoretic construction to evaluate the relative contributions of each logic-tree level to the overall UCERF3-TI epistemic variance.
SHOW MORE

Citation: Santa Maria, J. T., Vazquez, L., & Jordan, T. H. (2020, 08). Covariance Analysis of the UCERF3-TI Logic Tree. Poster Presentation at 2020 SCEC Annual Meeting.