Group A, Poster #113, Fault and Rupture Mechanics (FARM)

Adjoint Rupture Dynamics and Gradient-Based Dynamic Source Inversions

Eric M. Dunham, Vidar Stiernström, & Martin Almquist
Poster Image: 

Poster Presentation

2024 SCEC Annual Meeting, Poster #113, SCEC Contribution #13538 VIEW PDF
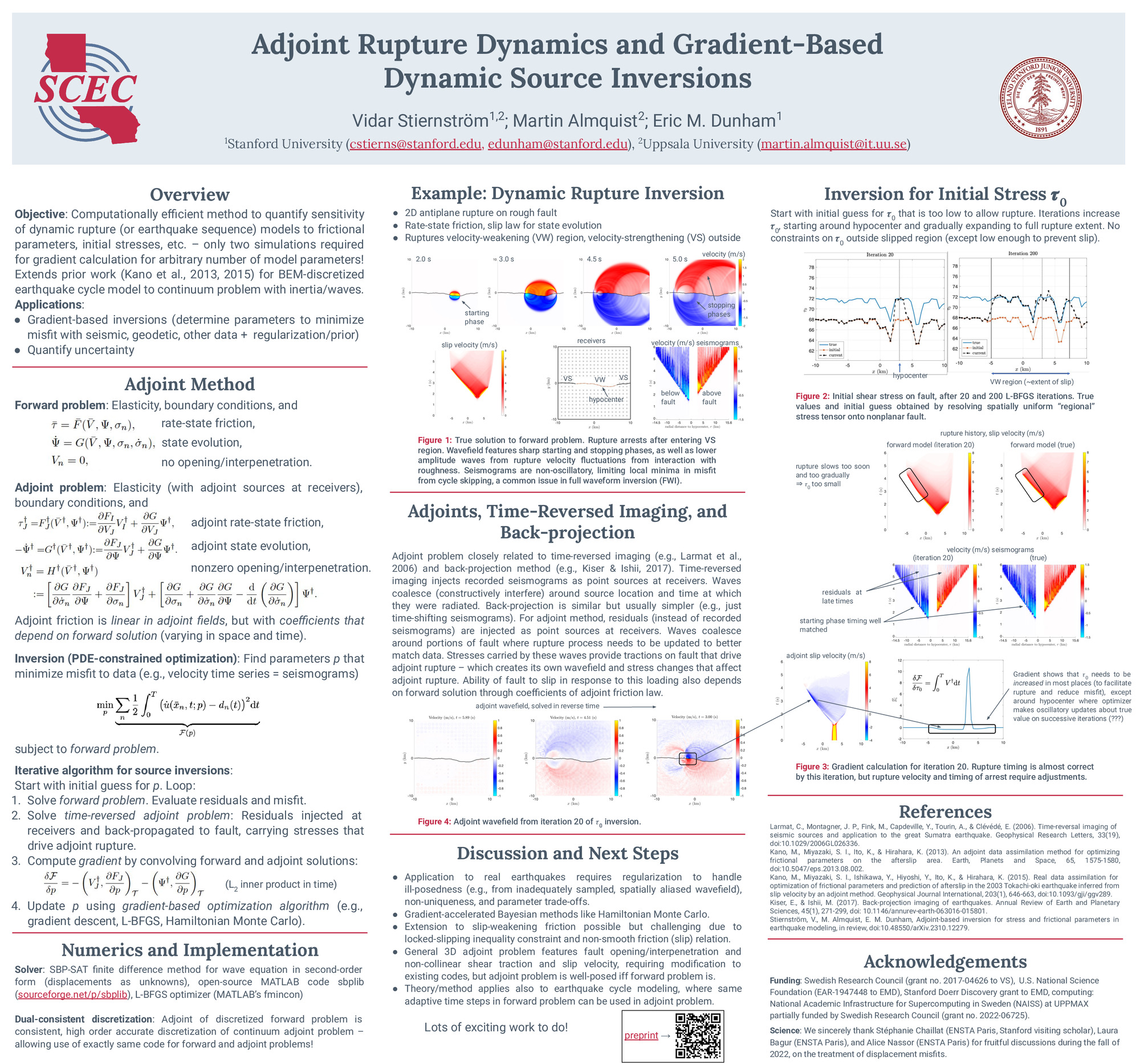
Dynamic rupture models provide constraints on the initial stresses and frictional parameters that control rupture propagation and ground motion. Earthquake sequence models extend this framework to slow slip events, afterslip, and nucleation. Dynamic rupture and afterslip inversions, which minimize the misfit to data, have been done by manual parameter tuning or computationally expensive Bayesian methods. Here we introduce an alternative method that combines one forward and one adjoint solution to calculate the gradient with respect to model parameters (initial stresses and frictional parameters). We use rate-state friction in the forward problem. The adjoint problem requires solving the same... elasticity problem but with the fault governed by a linearized rate-state friction law whose coefficients are functions of the forward solution. Residuals at measurement locations (e.g., seismometers or GNSS stations) are backpropagated to the fault, providing forcing that drives an adjoint rupture. Furthermore, for forward problems involving fault normal stress changes (but no opening), the adjoint problem features nonzero fault opening. Time convolution of the forward and adjoint solutions on the fault provides components of the gradient of the misfit with respect to model parameters. The gradient can be used in gradient-based optimization methods such as BFGS or Hamiltonian Monte Carlo.

We present theoretical and computational results to demonstrate the method. The theory is for the general 3D problem (encompassing dynamic rupture and earthquake sequence modeling), whereas computational examples are for a 2D antiplane shear dynamic rupture. We use a dual-consistent summation-by-parts finite difference discretization, which permits use of the same code for forward and adjoint modeling (the latter performed in reverse time). Dual consistency guarantees that the discrete gradient is exact and that the discrete adjoint problem is a consistent discretization of the continuum adjoint problem. We demonstrate how the method can be used to recover initial stress and frictional parameters. These parameters are constrained only on parts of the fault that slip; parameters outside this region are instead bounded to values that inhibit rupture. Application to real events will require regularization or Bayesian samping to handle parameter trade-offs and nonuniqueness.
SHOW MORE

Citation: Dunham, E. M., Stiernström, V., & Almquist, M. (2024, 09). Adjoint Rupture Dynamics and Gradient-Based Dynamic Source Inversions. Poster Presentation at 2024 SCEC Annual Meeting.
Keywords: adjoint, inversion, dynamic rupture, earthquake cycle
Relevant SCEC Themes:
Advanced Modeling Frameworks
Research Computing