Poster #167, Fault and Rupture Mechanics (FARM)
Exploring the effects of a sedimentary basin on the earthquake cycle using a non-stiff finite difference method for elastodynamics
Poster Image:
Poster Presentation
2021 SCEC Annual Meeting, Poster #167, SCEC Contribution #11587 VIEW PDF
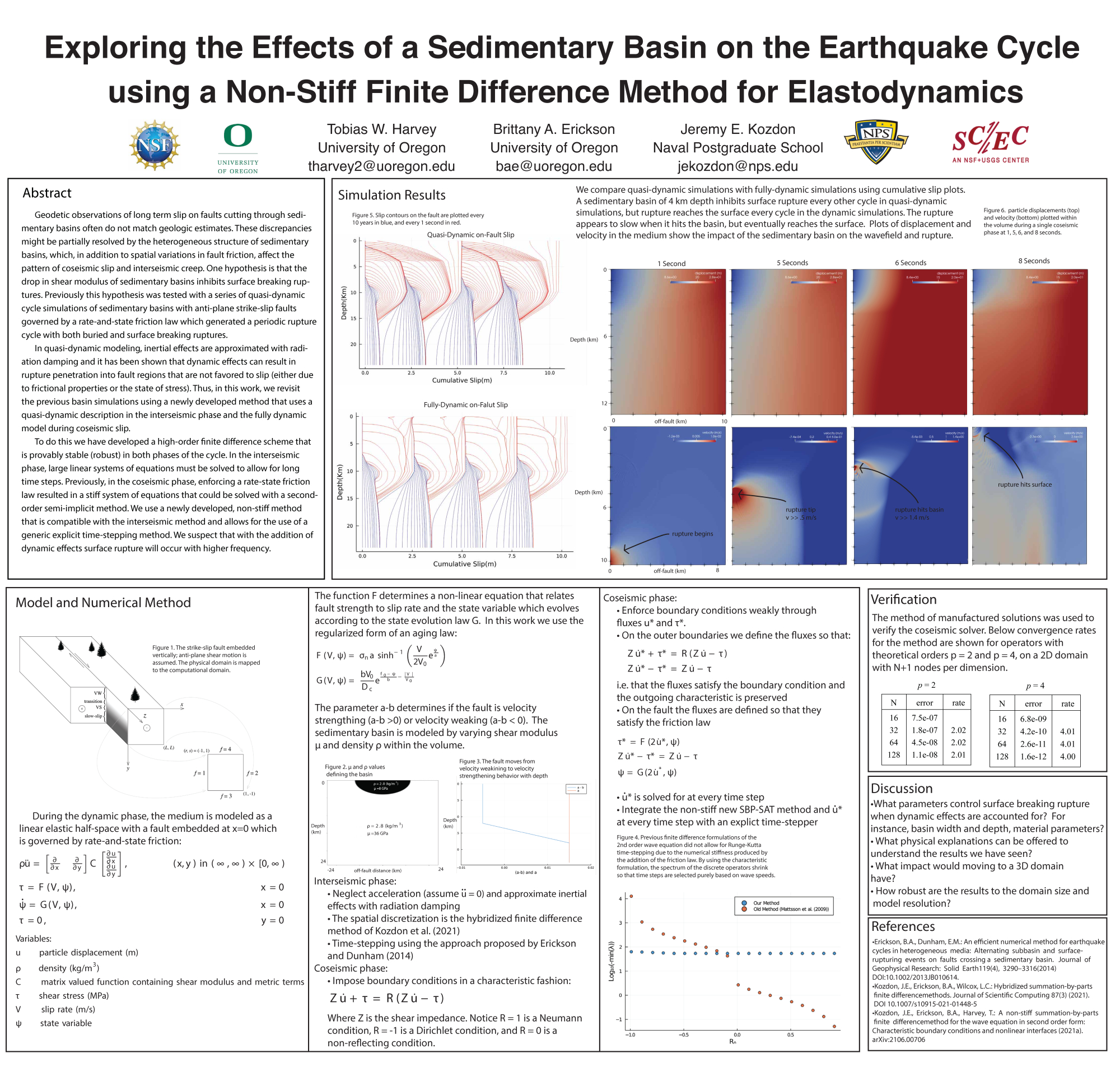
urface breaking ruptures.
In quasi-dynamic modeling, inertial effects are approximated with radiation damping and it has been shown that dynamic effects can result in rupture penetration into fault regions that are not favored to slip (either due to frictional properties or the state of stress). Thus, in this work, we revisit the previous basin simulations using a newly developed method that uses a quasi-static description in the interseismic phase and the fully dynamic model during coseismic slip.
To do this we have developed a high-order finite difference scheme that is provably stable (robust) in both phases of the cycle. In the interseismic phase, large linear systems of equations must be solved to allow for large time steps. Previously, in the coseismic phase, enforcing a rate-state friction law resulted in a stiff system of equations that could be solved with a second-order semi-implicit method. We use a newly developed, non-stiff method that is compatible with the interseismic method and allows for the use of a generic explicit time-stepping method. We suspect that with the addition of dynamic effects surface rupture will occur with higher frequency.
SHOW MORE
In quasi-dynamic modeling, inertial effects are approximated with radiation damping and it has been shown that dynamic effects can result in rupture penetration into fault regions that are not favored to slip (either due to frictional properties or the state of stress). Thus, in this work, we revisit the previous basin simulations using a newly developed method that uses a quasi-static description in the interseismic phase and the fully dynamic model during coseismic slip.
To do this we have developed a high-order finite difference scheme that is provably stable (robust) in both phases of the cycle. In the interseismic phase, large linear systems of equations must be solved to allow for large time steps. Previously, in the coseismic phase, enforcing a rate-state friction law resulted in a stiff system of equations that could be solved with a second-order semi-implicit method. We use a newly developed, non-stiff method that is compatible with the interseismic method and allows for the use of a generic explicit time-stepping method. We suspect that with the addition of dynamic effects surface rupture will occur with higher frequency.
SHOW MORE























































