SCEC2021 Poster #253: Modified estimation and forecasting of the hierarchical space-time ETAS (HIST-ETAS) model for earthquake catalogs in a wide area possessing long- and short-term incompleteness

Poster #253, Earthquake Forecasting and Predictability (EFP)

Modified estimation and forecasting of the hierarchical space-time ETAS (HIST-ETAS) model for earthquake catalogs in a wide area possessing long- and short-term incompleteness

Poster Image:

Poster Presentation

2021 SCEC Annual Meeting, Poster #253, SCEC Contribution #11394 VIEW PDF

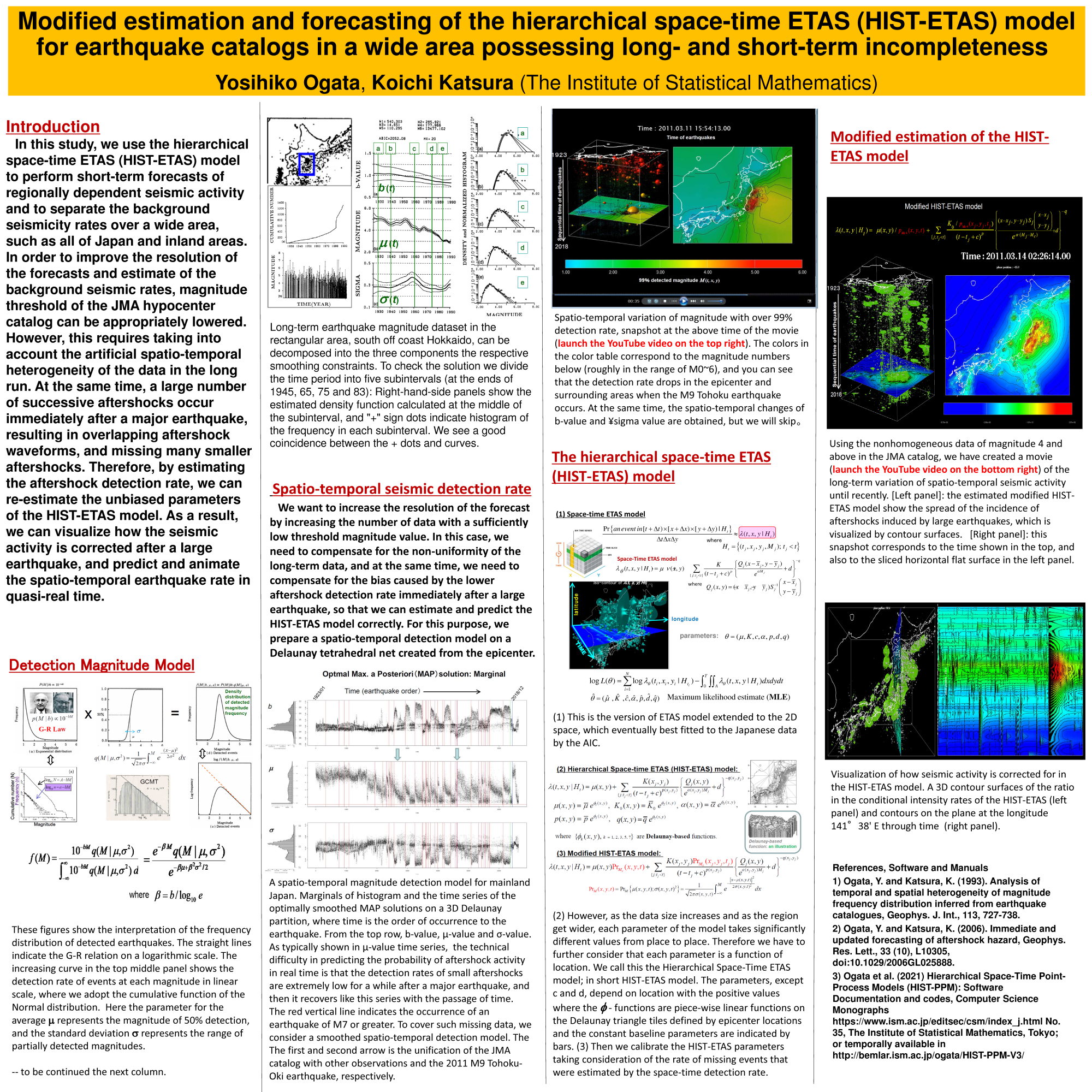
In this study, we use the hierarchical spatio-temporal ETAS (HIST-ETAS) model to make short-term forecasts of region-dependent seismic activity and to separate background seismicity rates over a wide area, such as all of Japan and inland areas. In order to improve the resolution of the forecasts and background seismic rates, the threshold magnitude value of the JMA seismic source catalog can be appropriately lower. However, this requires taking into account the artificial spatio-temporal heterogeneity of the data in the long run. At the same time, a large number of successive aftershocks occur immediately after a major earthquake, resulting in overlapping aftershock waveforms and missing sma...ller aftershocks. Therefore, by estimating the aftershock detection rates that decreases after large earthquakes, we can re-estimate the unbiased parameters of the HIST-ETAS model. As a result, we can visualize how the seismic activity is corrected after large earthquakes, and predict and animate the spatio-temporal earthquake rates in quasi-real time.

References and Software with Manuals　
1) Ogata, Y. and Katsura, K. (1993). Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues, Geophys. J. Int., 113, 727-738.

2) Ogata, Y. and Katsura, K. (2006). Immediate and updated forecasting of aftershock hazard, Geophys. Res. Lett., 33 (10), L10305, doi:10.1029/2006GL025888.

3) Ogata et al. (2021) Hierarchical Space-Time Point-Process Models (HIST-PPM): Software Documentation and codes, Computer Science Monographs https://www.ism.ac.jp/editsec/csm/index_j.html No. 35, The Institute of Statistical Mathematics, Tokyo; or temporally available in http://bemlar.ism.ac.jp/ogata/HIST-PPM-V3/．
SHOW MORE

Lightning Talk

Full Presentation

Citation: Ogata, Y., & Katsura, K. (2021, 08). Modified estimation and forecasting of the hierarchical space-time ETAS (HIST-ETAS) model for earthquake catalogs in a wide area possessing long- and short-term incompleteness. Poster Presentation at 2021 SCEC Annual Meeting.

Keywords: space-time ETAS model, hypocenter detection rates, 2D and 3D Delaunay tessellation

Relevant SCEC Themes:

Probabilistic Seismic Hazard Analysis

Operational Earthquake Forecasting

Post-Earthquake Rapid Response