Group A, Poster #227, Ground Motions (GM)
Ground Motion Synthesis via Generative Adversarial Network Operators: A Paradigm Shift from Simulated Broadband Ground Motions?
Poster Image:
Poster Presentation
2022 SCEC Annual Meeting, Poster #227, SCEC Contribution #12258 VIEW PDF
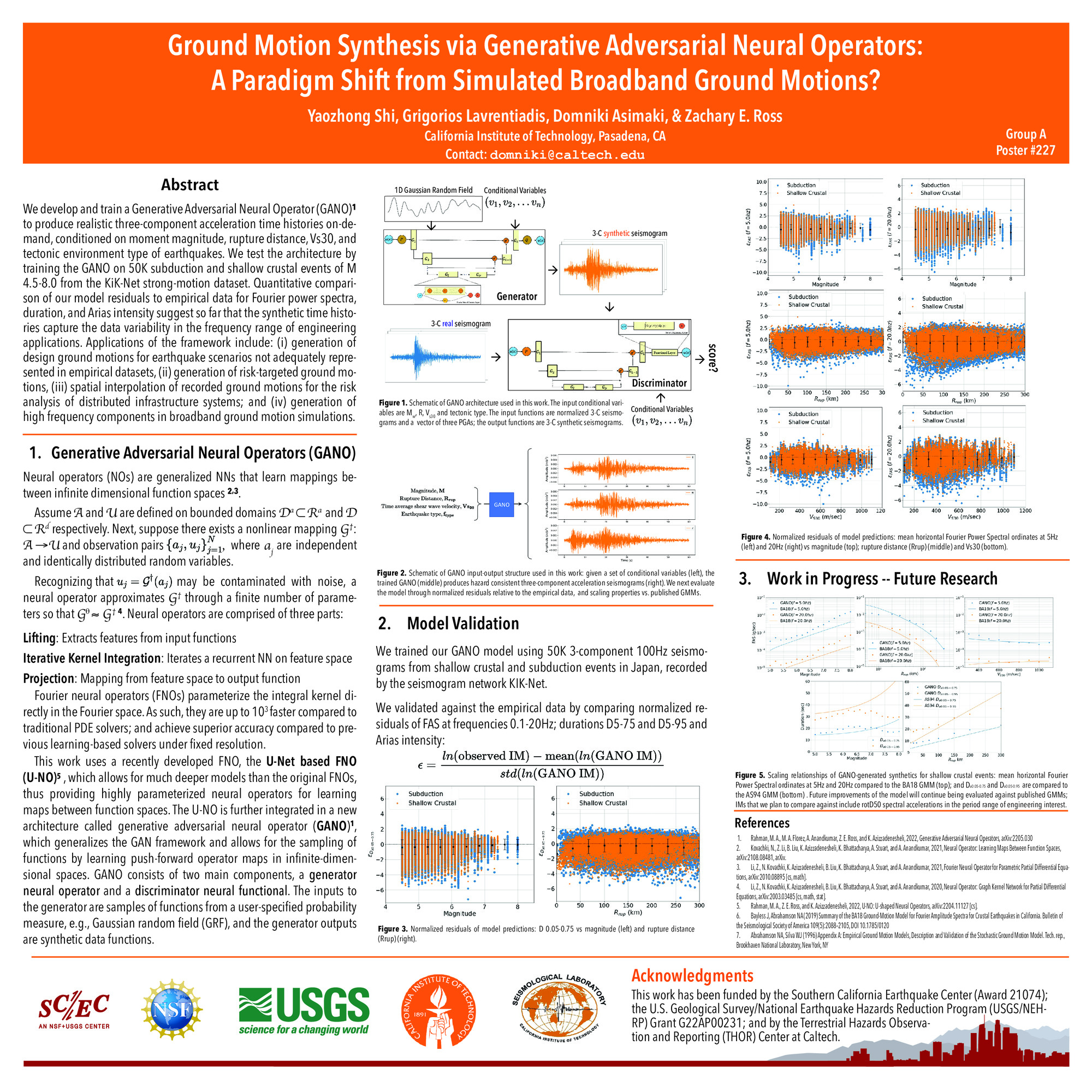
We present a novel approach for developing on-demand synthetic ground motions for engineering applications. Leveraging the increase of ground-motion data from seismic networks, the availability of physics-based ground motion simulations, and recent advancements in Machine Learning, we train a Generative Adversarial Network Operator (GANO) (Rahman et al., 2022) to produce realistic three-component acceleration time histories conditioned on moment magnitude, rupture distance, Vs30, tectonic environment type of earthquakes. Neural operators allow for the sampling of functions by learning push-forward operator maps in infinite-dimensional spaces, rendering our model resolution-invariant.
We verify the architecture by training the GANO on ground motions produced by stochastic time-domain and frequency-domain approaches (Boore 2003; Thrainsson and Kiremidjian 2002; Bayless and Abrahamson 2019). We illustrate that the proposed framework can recover the imposed magnitude, distance, and duration scaling. We then harvest 50K events of M 4.5 to 8.0 from the KiK-Net strong-motion dataset and train the GANO for shallow crustal and subduction events. Qualitative comparison of our results to empirical ground-motion models (GMMs) for spectral accelerations, duration, Arias intensity, and phase derivative distributions suggests so far that the GANO-generated time histories capture scaling relationships in the 0.1 to 50 Hz frequency range, which is important for their adoption in engineering applications.
Potential applications of the presented framework include: (i) generation of design ground motions for earthquake scenarios not adequately represented in empirical datasets, (ii) generation of risk-targeted ground motions, and (iii) spatial interpolation of recorded ground motions for the risk analysis of distributed infrastructure systems.
Bayless, J., & Abrahamson, N. A. (2019). Summary of the BA18 ground‐motion model for Fourier amplitude spectra for crustal earthquakes in California. BSSA 109(5), 2088-2105.
Boore, D. M. (2003). Simulation of ground motion using the stochastic method. PAGEOPH, 160(3), 635-676.
Thrainsson, H., & Kiremidjian, A. S. (2002). Simulation of digital earthquake accelerograms using the inverse discrete Fourier transform.EESD, 31(12), 2023-2048.
Rahman, M. A., M. A. Florez, A. Anandkumar, Z. E. Ross, and K. Azizzadenesheli, 2022, Generative Adversarial Neural Operators, arXiv:2205.03017
We verify the architecture by training the GANO on ground motions produced by stochastic time-domain and frequency-domain approaches (Boore 2003; Thrainsson and Kiremidjian 2002; Bayless and Abrahamson 2019). We illustrate that the proposed framework can recover the imposed magnitude, distance, and duration scaling. We then harvest 50K events of M 4.5 to 8.0 from the KiK-Net strong-motion dataset and train the GANO for shallow crustal and subduction events. Qualitative comparison of our results to empirical ground-motion models (GMMs) for spectral accelerations, duration, Arias intensity, and phase derivative distributions suggests so far that the GANO-generated time histories capture scaling relationships in the 0.1 to 50 Hz frequency range, which is important for their adoption in engineering applications.
Potential applications of the presented framework include: (i) generation of design ground motions for earthquake scenarios not adequately represented in empirical datasets, (ii) generation of risk-targeted ground motions, and (iii) spatial interpolation of recorded ground motions for the risk analysis of distributed infrastructure systems.
Bayless, J., & Abrahamson, N. A. (2019). Summary of the BA18 ground‐motion model for Fourier amplitude spectra for crustal earthquakes in California. BSSA 109(5), 2088-2105.
Boore, D. M. (2003). Simulation of ground motion using the stochastic method. PAGEOPH, 160(3), 635-676.
Thrainsson, H., & Kiremidjian, A. S. (2002). Simulation of digital earthquake accelerograms using the inverse discrete Fourier transform.EESD, 31(12), 2023-2048.
Rahman, M. A., M. A. Florez, A. Anandkumar, Z. E. Ross, and K. Azizzadenesheli, 2022, Generative Adversarial Neural Operators, arXiv:2205.03017







































